Page 22 - 高中数学小题狂做·教材梳理

52

高中数学 ·教材梳理

三、 填空题 中, AB=

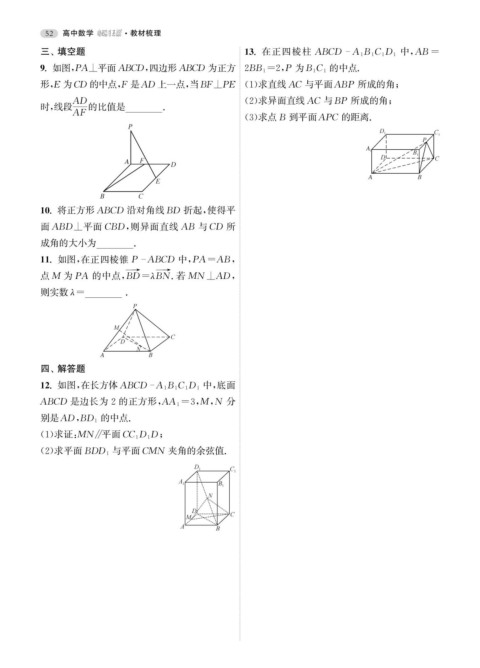
13. 在正四棱柱 ABCD A 1 B 1 C 1 D 1

的中点.
9. 如图, PA⊥平面ABCD , 四边形ABCD 为正方 2BB 1=2 , P 为B 1 C 1
形, E 为CD 的中点, F 是AD 上一点, 当BF⊥PE ( 1 ) 求直线AC 与平面ABP 所成的角;
AD ( 2 ) 求异面直线AC 与BP 所成的角;
时, 线段 的比值是 .
AF
( 3 ) 求点B 到平面APC 的距离.

10. 将正方形ABCD 沿对角线BD 折起, 使得平

面ABD⊥平面CBD , 则异面直线 AB 与CD 所

成角的大小为 .

11. 如图, 在正四棱锥 P ABCD 中, PA=AB ,
→ →
点 M 为PA 的中点, BD=λBN. 若 MN ⊥AD ,

则实数 λ= .

四、 解答题

中, 底面

12. 如图, 在长方体ABCD A 1 B 1 C 1 D 1
ABCD 是边长为2的正方形, AA 1=3 , M , N 分
的中点.
别是AD , BD 1
( 1 ) 求证: MN∥ 平面CC 1 D 1 D ;

与平面CMN 夹角的余弦值.
( 2 ) 求平面BDD 1