Page 27 - 高考物理小题狂做·基础篇·Ⅱ

第二章 相互作用 牛顿运动定律

解决动态平衡常用方法
1. 解析法

如果物体受到多个力的作用, 可进行正交分解, 利用解析法, 建
立平衡方程, 找函数关系, 根据自变量的变化确定因变量的变化, 还

可由数学知识求极值或者根据物理临界条件求极值.

2. 图解法
物体受三个力平衡: 一个力恒定、 另一个力的方
向恒定时可用此法. 由三角形中边长的变化知力的大

小的变化, 还可判断出极值.

例: 挡板 P 由竖直位置绕 O 点逆时针向水平位
置缓慢旋转时小球受力的变化( 如图) .

3. 相似三角形法

物体受三个力平衡: 一个力恒定、 另外两个力的方向同时变化,

当所作“ 力的矢量三角形” 与空间的某个“ 几何三角形” 总相似时用此
法( 如图) .

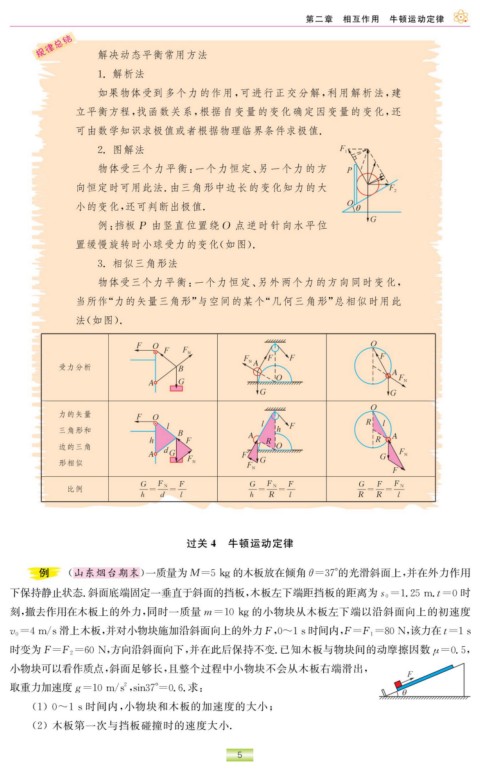
受力分析

力的矢量
三角形和
边的三角

形相似

G F N F G F N F G F F N
比例 = = = = = =
h d l h R l R R l

过关4 牛顿运动定律

例 ( 山东烟台期末) 一质量为 M=5k g 的木板放在倾角 θ=37° 的光滑斜面上, 并在外力作用

下保持静止状态. 斜面底端固定一垂直于斜面的挡板, 木板左下端距挡板的距离为 s 0=1.25m.t=0时

刻, 撤去作用在木板上的外力, 同时一质量 m=10k g 的小物块从木板左下端以沿斜面向上的初速度

v 0=4m / s滑上木板, 并对小物块施加沿斜面向上的外力F , 0~1s时间内, F=F 1=80N , 该力在 t=1s

时变为F=F 2=60N , 方向沿斜面向下, 并在此后保持不变. 已知木板与物块间的动摩擦因数 =0.5 ,
μ
小物块可以看作质点, 斜面足够长, 且整个过程中小物块不会从木板右端滑出,
取重力加速度 g=10m / s , sin37°=0.6. 求:

2

( 1 ) 0~1s时间内, 小物块和木板的加速度的大小;

( 2 )木板第一次与挡板碰撞时的速度大小.

5