Page 53 - 高考物理小题狂做·基础篇·新课标（新教材老高考版）

第二章 相互作用 牛顿运动定律
面的压力大于B 木块对斜面的压力, A 错误, B正确; 设小球的质量为 m , 以小球与 A 整体为研究
对象, 由平衡条件可得A 木块受到的摩擦力 f A = ( M +m )· sinα ; 同理, 以小球与 B 整体为研
g
究对象, 得到B 木块受到的摩擦力 f B= ( M+m ) sinα , 则 f A= f B C 、 D 错误.
,
g

甲 乙

受力分析和运用平衡条件列式.
确定研究对象是解答平衡问题的首要环节, 如果两个或两个以上的
物体所组成的系统处于平衡时, 可采用整体法求解, 关键要正确地进行

过关4 牛顿运动定律

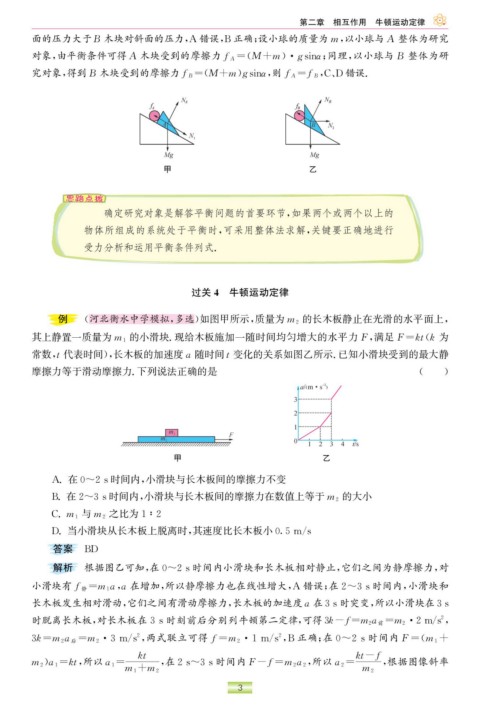
的长木板静止在光滑的水平面上,
例 ( 河北衡水中学模拟, 多选) 如图甲所示, 质量为 m 2
的小滑块. 现给木板施加一随时间均匀增大的水平力F , 满足F=kt ( k 为
其上静置一质量为 m 1
常数, t 代表时间), 长木板的加速度a 随时间 t 变化的关系如图乙所示. 已知小滑块受到的最大静

摩擦力等于滑动摩擦力. 下列说法正确的是 ( )

甲 乙

A. 在0~2s时间内, 小滑块与长木板间的摩擦力不变

的大小

B. 在2~3s时间内, 小滑块与长木板间的摩擦力在数值上等于 m 2

之比为1∶2
C.m 1 与 m 2

D. 当小滑块从长木板上脱离时, 其速度比长木板小0.5m / s
答案 BD
解析 根据图乙可知, 在0~2s时间内小滑块和长木板相对静止, 它们之间为静摩擦力, 对

小滑块有 f静=m 1 a , a 在增加, 所以静摩擦力也在线性增大, A 错误; 在2~3s时间内, 小滑块和

长木板发生相对滑动, 它们之间有滑动摩擦力, 长木板的加速度 a 在3s时突变, 所以小滑块在3s
·

时脱离长木板, 对长木板在3s时刻前后分别列牛顿第二定律, 可得3k- f=m 2 a 前=m 2 2m / s ,

2

·

3k=m 2 a后=m 2 3m / s , 两式联立可得 f=m 2 1m / s , B 正确; 在0~2s时间内 F= ( m 1+
·
2
2
kt kt- f
) , 根据图像斜率
m 2 a 1=kt , 所以a 1= , 在2s~3s时间内F- f=m 2 a 2 , 所以a 2=
m 1+m 2 m 2
3